1 地震响应计算模型

1．1结构概况

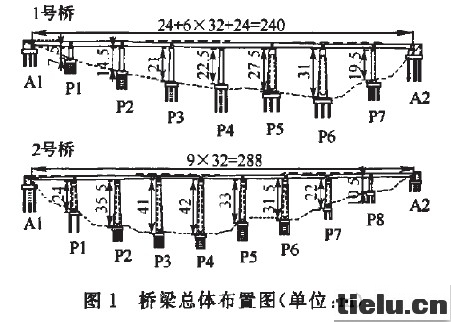
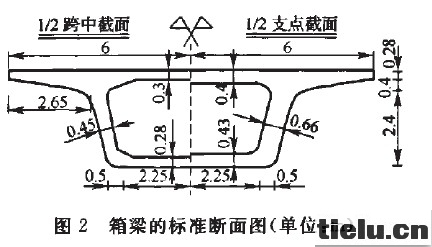
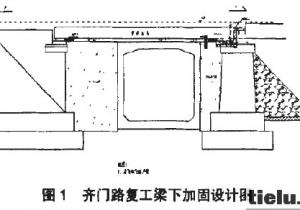
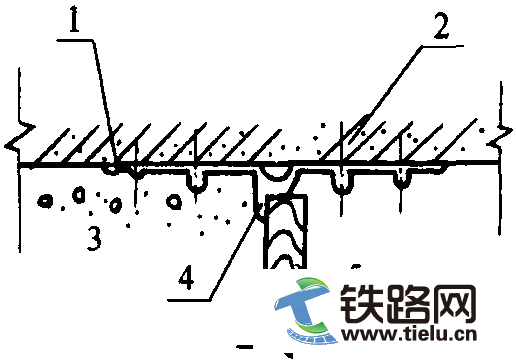
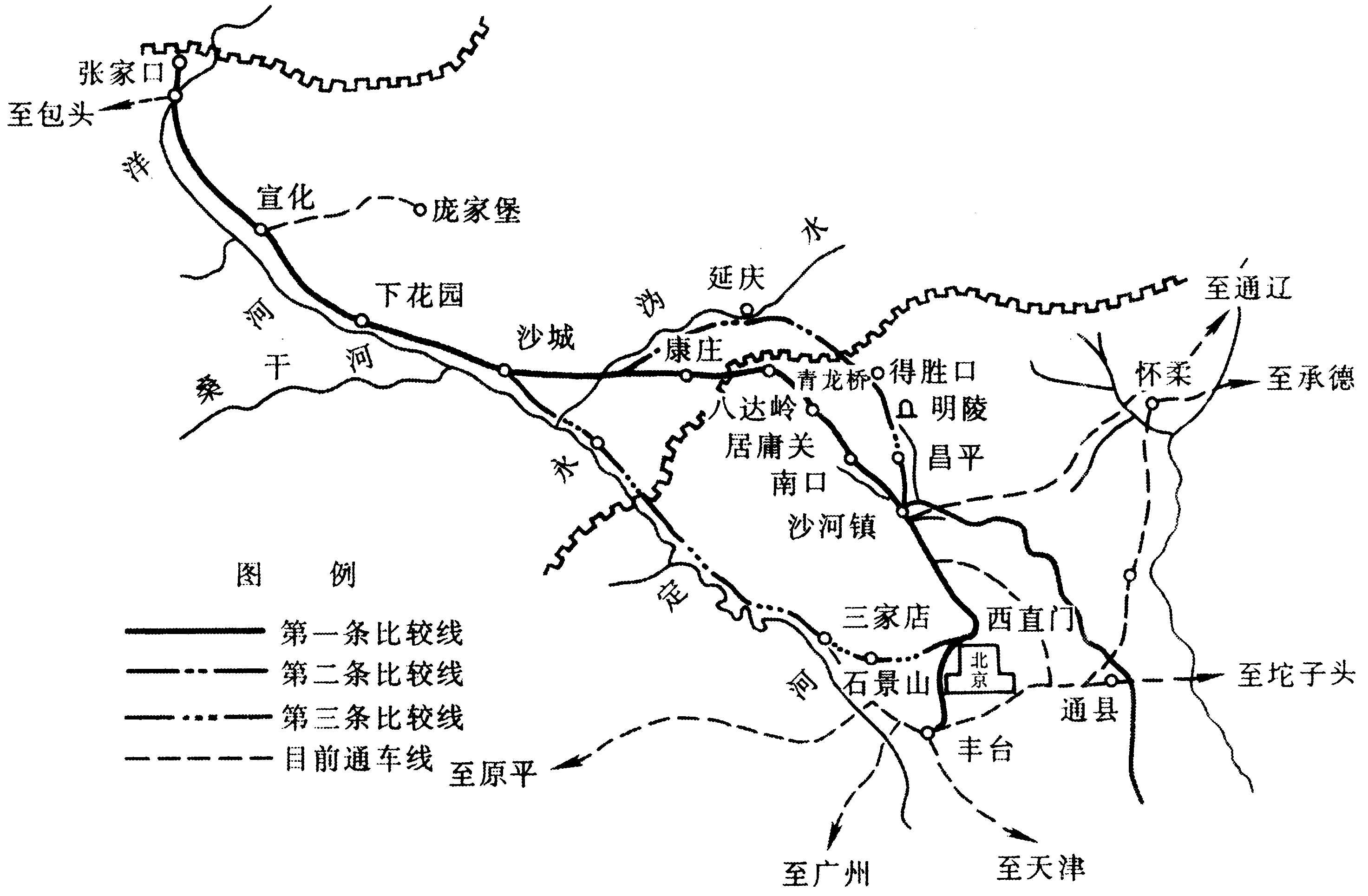
为研究轨道约束对铁路减隔震桥梁的地震响应影响，本文选取图1所示的8度区采用减隔震技术设计的两座实际铁路桥梁为对象进行分析。上部结构为预应力混凝土简支箱梁桥，箱梁标准断面如图2所示。其中，l号桥的孔径布置为(24+6×32+24)m，墩高75～310 m，采用摩擦摆式支座作为减隔震装置，支座编号从左边桥台(A1)至右端桥台(A2)依次为1～16(每个桥墩对应两排支座，每个桥台对应一排支座)。2号桥的孔径布置为9×32 m，墩高105～42 m，采用橡胶支座和E型钢阻尼构件组合作为减隔震支座。支座编号从左边桥台(A1)至右端桥台(A2)依次为1～18。

1．2计算模型

结构地震响应采用图3所示的桥梁-轨道一体化计算模型，减隔震装置变形和道床纵向位移阻力采用双线性弹簧单元，钢轨、主梁用线弹性梁单元。根据两座桥梁的设计条件，桥墩按罕遇地震条件下不进入塑性设计，故桥墩也采用弹性梁单元模拟。

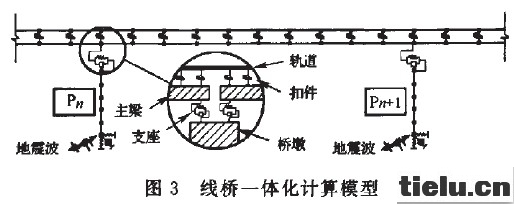
1．2．1粱-轨间的相互作用

轨道与桥梁间的相互作用通常由道床纵向阻力来描述。根据国内外实测资料，道床纵向阻力具有如图4所示的理想弹塑性变形特性。当轨道与道床相对位移小于2 mm左右时，道床纵向阻力与相对位移之间呈线性关系，当相对位移超过2 mm以后阻力不再随变形增加。图中U为轨道与桥梁之间发生相对滑动的位移，Fu为轨道滑动时的道床单位长度阻力即“道床阻力系数”。道床屈服纵向阻力有较大的离散性，与轨枕类型、道床种类、断面尺寸、捣固状态及道床不洁程度等因素有关，无载时约在10～20kN／m之间。

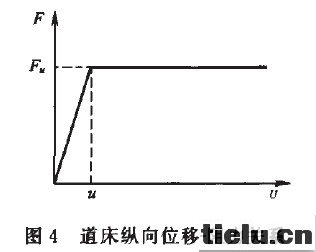
1．2．2减隔震装置的力学模型

图5为摩擦摆式支座的结构形式和力学计算模型，这种支座是利用球面滑动提供恢复刚度和摩擦吸收能量。支座离开平衡点时受到的水平分力F为：

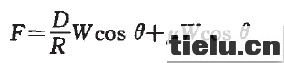
当口较小时，水平分力为

式中：W为支座竖向反力；D为水平摆动距离；R为滑动面曲率半径；p为滑动面摩擦系数；角度为中心滑块位置摆角。

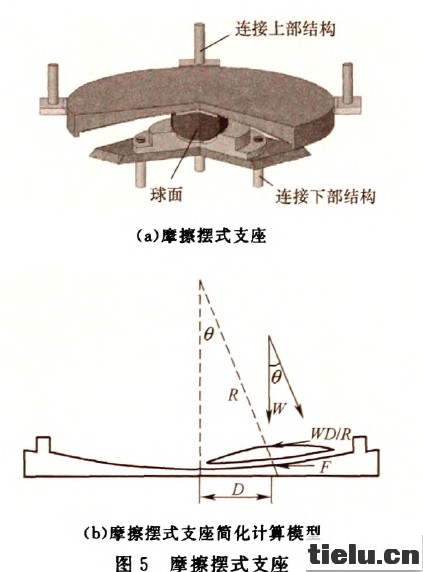
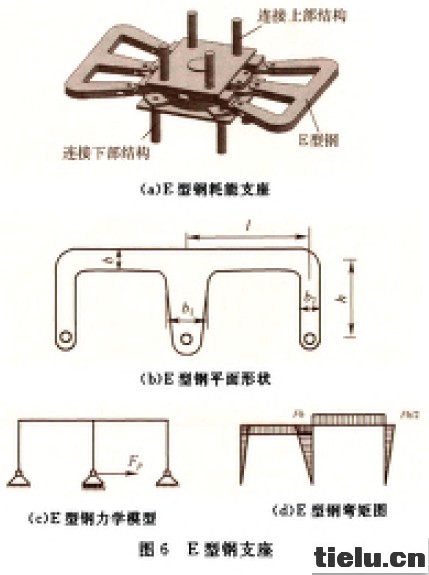
图6为E型钢耗能装置的结构形式和力学计算模型，它是一种普通盆式橡胶支座与弹塑性软钢阻尼元件E型钢组合一起的减隔震装置。当普通支座发生地震变形时，连接在支座上下两端的E型钢元件由于弹塑性变形吸收地震能量，降低地震作用。


2 结论

本文以高速铁路客运专线上两座采用不同减隔震装置的简支梁桥为对象。探讨了轨道约束对桥梁动力特性和地震响应的影响，通过多条地震波输入时的计算结果分析，得到以下几点结论：

（1）铁路减隔震桥梁当考虑轨道影响时，随着道床阻力系数的增大，桥梁纵向的自振频率也随之增大，初期变化较明显，但后期增大趋缓，并逐渐趋于稳定。相对于高阶振型而言，低阶振型的频率随道床阻力系数稳定较快。

（2）当道床阻力系数超过10 kN／m时，道床阻力系数增加对结构自振频率及地震响应影响较小。

（3）轨道对铁路减隔震桥梁的主粱纵向地震位移、减隔震支座的地震位移以及减隔震支座的累计耗能有一定影响，影响规律与桥梁的结构形式、输入地震波等许多因素有关，大致为不考虑轨道时地震位移的50％～150％。但是，对墩底的最大地震剪力影响很小。

根据上述结果，考虑到地震波的随机性、道床摩阻力的离散性以及边界条件、减隔震装置工作原理的差异，建议铁路减隔震桥梁在进行抗震设计时应考虑轨道约束的不利影响，以确保减隔震装置的作用。