当跨度较大时,横梁面外弯曲引起的应力相当大,给设计造成困难。本文针对纵横梁体系结合桥面桥梁,从桥面系变形协调出发,推导横梁面外弯曲问题的计算公式,分析横梁面外弯曲产生的主要原因和影响因素,提出改善桥面系受力状态的思路和方法。
1横梁面外弯曲问题的提出
横梁的面外弯曲问题在一座跨长江的四线三主桁斜拉桥(下称TX桥)下层铁路桥结合桥面设计时,变得相当严重,成为铁路桥面系设计的难点之一,引起关注。
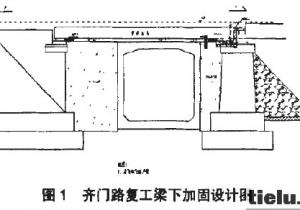
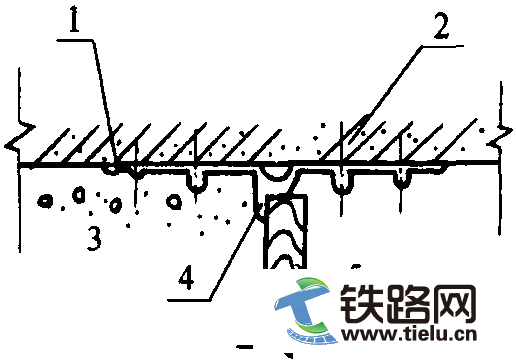
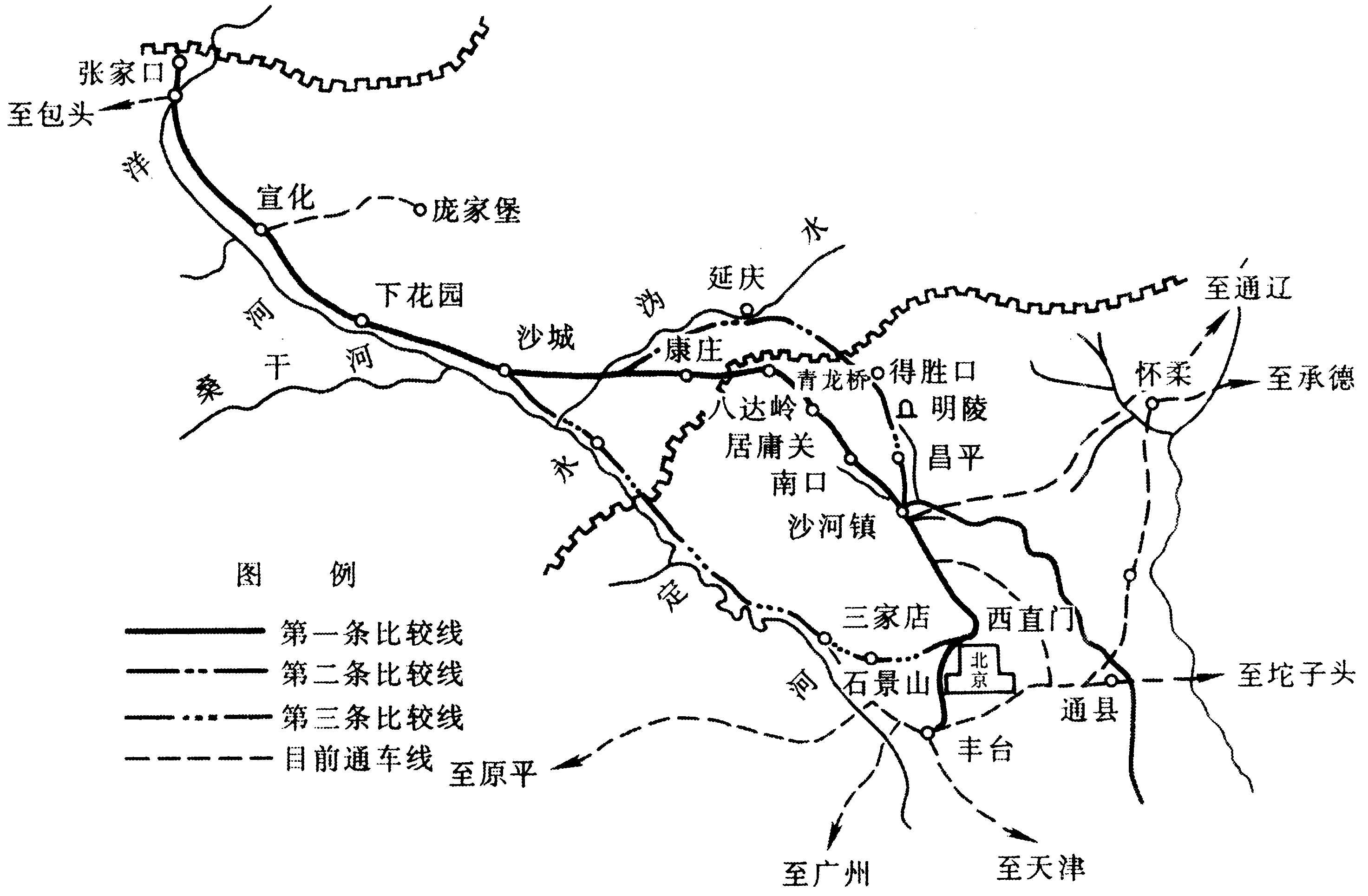
该桥主桥为双塔三索面三主桁公铁两用斜拉桥,桥跨布置为98m+196m+504m+196m+98m,分上下两层,上层为6车道公路,下层为4线铁路,其中两线客运专线,两线Ⅰ级铁路干线,分别分布于中主桁两侧。桁宽15m+15m=30m,节间长为14m。桥梁主体结构见图1。铁路桥面采用钢纵、横梁体系、混凝土桥面板仅与纵梁相结合的有砟桥面。每线铁路下设两片纵梁,间距为2m。纵梁为工字形截面,高为1.7m。铁路横梁为工字形截面,高为2.7m。混凝土道砟槽板厚为25cm,两侧设1m高挡砟板。

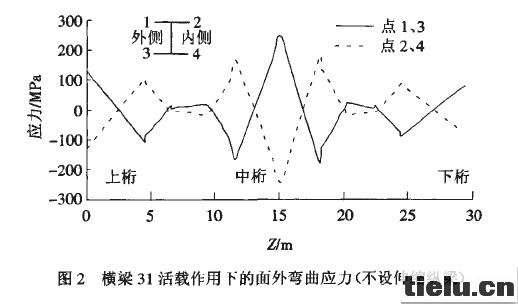
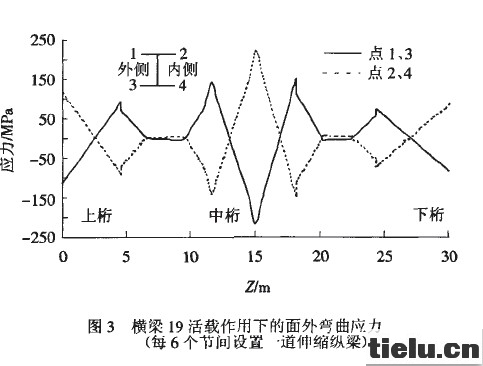
铁路桥面最早方案是不设伸缩纵梁或每6个节间设置一道伸缩纵梁。有限元分析结果表明:在主力和附加力作用下,这两种结构的主桁各杆件和斜拉索、塔、公路桥面等构件的强度、刚度都能满足规范的要求,但铁路桥面横梁的面外弯曲过大,横梁的水平弯曲引起横梁很大的弯曲应力。在活载单独作用下,不设伸缩纵梁时,最大水平挠度发生在横梁达6.8mm,由水平弯曲引起的横梁应力就达249MPa,见图2。每6个节间设置一道伸缩纵梁时,最大水平弯曲发生在横梁19到横梁24的节段,该节段最外两根横梁最大水平挠度达到6.0mm,由水平弯曲引起的最大应力为219MPa,见图3。若加上竖向弯曲应力以及恒载、附加力作用下的应力,许多横梁的应力将远远超限。
设计单位曾提出许多改进方法,如把横梁改成箱形截面,设置制动撑,每5节间或4节间设一道伸缩纵梁等,但都不能解决该问题。若把横梁改成箱形截面,增大面外抗弯刚度,则其面外弯矩也跟着增大,而横梁面外弯曲应力下降不明显。设置制动撑后,横梁的面外弯曲及由此导致应力有效降低,但纵梁的应力明显增加,纵梁成为控制桥面系设计的主要因素。最后每2个节间设置一道伸缩纵梁才解决问题。
纵横梁体系结合桥面在84m、96m下承式简支钢桁梁桥、140m钢箱系杆拱桥上都已成功应用,虽然也有横梁的面外弯曲问题,但问题并不严重,处理并不困难,因而未引起特别关注。为何在TX桥上横梁面外弯曲问题会如此严重,当6个节间设一道伸缩纵梁时,桥面系连续长度也只有84m,为何还不行,甚至连续长度为5节间、4节间甚至3节间时还不行,直至减至2节间(28m)时才能满足强度要求?本文将对此进行剖析。
2横梁面外弯曲应力的理论公式
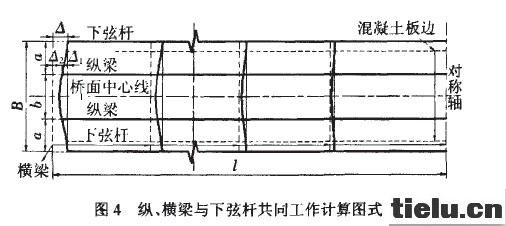
设桥面系两个伸缩纵梁间的连续长度为2l,取其一半即长度为l的桥面系为研究对象,见图4,右边是对称轴(即节段中间位置)无纵向位移,横梁不弯曲,左边是该段桥面系连续长度的端部,横梁水平弯曲最大。由此推导左端横梁的面外弯曲变形公式。
2.1桥面系变形协调条件
为简化计算,假定桥面系中有两片纵梁,横桥问受力对称,结构见图4,其中l、B、a、b见图4。

因现在都采用整体结点,横梁与下弦杆的连接接近刚结,但由于下弦杆并非绝对刚性,下弦结点可能在水平面内产生微小转动,横梁两端介于铰结与刚结之间。对横梁分别按刚结与铰结两种情况分析。
2.2横梁两端刚结时的计算公式
横梁面外弯曲的弯矩和变形见图5。
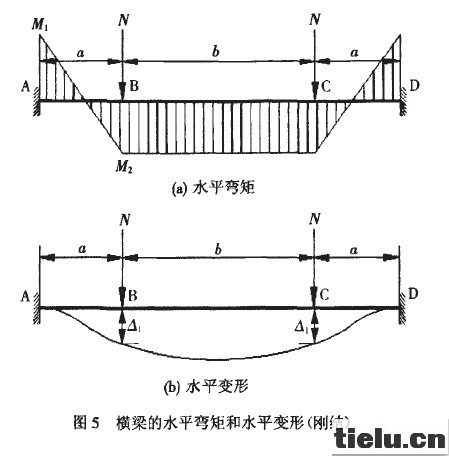
图中

2.3横梁两端铰结时的计算公式
横梁面外弯曲的弯矩和变形见图6。
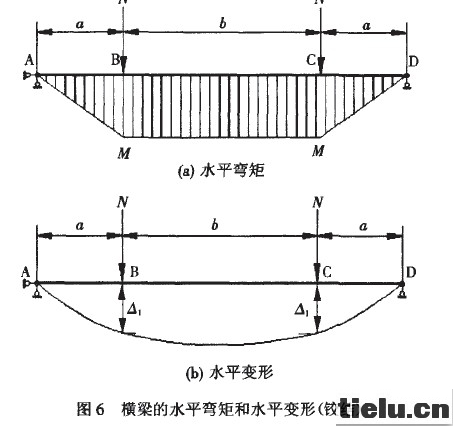
免责声明:本网站所刊载信息,不代表本站观点。所转载内容之原创性、真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考并自行核实。