Codden首次进行位于十字路口上高架桥曲线桥梁的抗震试验，李国豪则用有限元法分析了曲线桥梁的地震反应，提出了一种每节点8自由度的曲线梁单元，并将计算结果与直线梁单元模拟的计算结果进行了比较。在这之后，则有更多的学者对曲线桥梁的动力特性计算、时程分析、构造方面的问题进行了大量的研究。但是，对曲线桥梁的动力特性分析，主要针对公路曲线桥梁进行了大量的研究工作，对铁路曲线梁桥的动力分析进行得较少。

    土结构相互作用对系统的动力学参数有重要影响，进而影响结构的地震响应，因此，土的刚度及阻尼参数对桥梁结构地震响应的影响越来越受到人们的关注。在阪神地震后，日本在改订桥梁抗震规范时，已经把上部结构-基础-地基的相互作用作为一个重要因素来考虑。

    减隔震措施在我国铁路桥梁工程中已有应用，国内很多学者也对铁路桥梁的减隔震措施进行了很多相关研究，本文计算的曲线铁路梁桥便使用了研究相对较多的铅芯橡胶支座。本文基于M法，在不同的基础弹性刚度下，对具有硬土质基础的铁路隔震曲线梁桥在不同地震激励作用下进行了地震响应分析，研究了其地震响应的变化规律，取得了一些有价值的结果，为依据M法对具有硬土质基础的铁路曲线梁桥进行抗震设计提供了重要参考。

    1结构分析模型及地震激励的选取

    1.1结构分析模型

    以某隔震铁路连续曲线梁桥为例，研究基础弹性刚度对隔震曲线梁桥地震响应的影响。该桥为—3跨连续曲线梁桥，曲率半径为500m，跨径组合为35m+60m+35m，桥墩均为实心矩形截面，采用C30混凝土浇筑，其中墩高度为9m，边墩高度为10.5m。桥墩编号为1~4号，结果分析时以典型桥墩3号中墩为例。

    3号墩的基础为3x2的群桩基础，桩直径为1.2m，桩长25m，采用C30混凝土灌注。

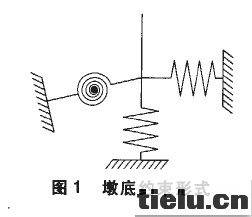
    计算时建立全桥模型，各墩底部约束方式如图1所示，以模拟基础弹性刚度。计算基于大型通用软件ANSYS，主梁采用BEAM44单元模拟，桥墩采用BEAM4单元模拟，铅芯橡胶支座采用COMBINE39单元模拟，基础对结构的影响通过矩阵单元MATRIX27单元实现。

    

    

    1.2铅芯橡胶支座力学模型

    铅芯橡胶支座（LRB）采用简化的双向恢复力-位移滞回理论模型，如图2所示。

    

    

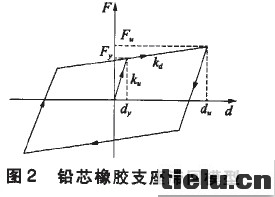
    其中，F，、d，分别为支座的屈服力和屈服位移；F、d。分别为支座的水平极限承载力和极限位移，k、kd则分别为支座的屈服前刚度和屈服后刚度；支座硬化比。

    1.3地震激励的选取

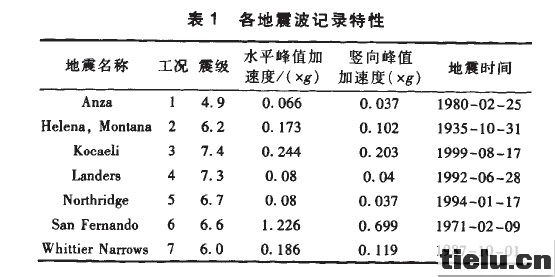
    该桥处于一类场地，场地基本设防烈度为8度，因此在分析中，选用了7条一类场地条件下的实际地震地面加速度记录作为激励输入。地震激励的输入方向则分别为两桥台连线方向、与两桥台连线垂直的水平方向和竖向。各地震波记录特性如表1所示。

    

    

    2基础弹性刚度对地震响应的影响研究

    2.1利用“M法”确定基础弹性刚度

    目前，我国铁路桥梁以及公路桥梁的设计规范中，当桩基础承受水平荷载、竖向荷载或弯矩的作用时，基础的刚度由“M法”计算得到。计算弹性支承刚度的具体步骤为：首先，根据桩基础的具体情况，计算确定各桩单桩桩顶刚度；其次，根据各桩的排列，利用式（1）~（4）确定基础的各个弹性刚度系数。

    

    本文分析的铁路曲线梁桥，依据“M法”计算得到m=30000kPa／n12时的基础刚度系数如表2所示。

    

    

    2.2不同基础弹性刚度下曲线梁桥的地震响应

    本例中的曲线梁桥所处场地为一类场地，根据3号桥墩所处位置的土层特性，按照规范规定，m取值范围为30000~80000kPa/m2．以m=30000kPa/m2时计算得到的基础弹性刚度值为基准，定义其他m值所对应的基础弹性刚度与m=30000kPa/m2时对应的基础弹性刚度值的比值为基础刚度变化系数。故该桥所处场地的基础刚度变化系数变化范围为1.0~2.667。同时，为了更好的研究基础刚度对曲线梁桥地震响应的影响规律，本文还对基础刚度变化系数在0.2~1.0变化时的情况进行了地震响应的计算。