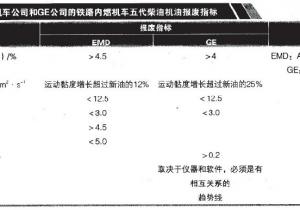
静态模型和动态模型
静态关系或静态特性:系统中各变量随时间变化缓慢,其对时间的变化率(导数)可忽略不计时,这些变量间的关系称为静态关系或静态特性,系统称为静态系统。相应的数学模型称为静态模型。
静态模型中不含有变量对时间的导数。
动态关系或动态特性:系统中变量对时间的变化率不可忽略,这时各变量之间的关系称为动态关系或动态特性,系统称为动态系统,相应的数学模型称为动态模型 。
控制系统中的数学模型绝大部分都指的是动态系统的数学模型。
状态空间描述或内部描述
不仅可以描述系统输入、输出之间的关系,而且还可以描述系统的内部特性。
它特别适用于多输入、多输出系统,
也适用于时变系统、非线性系统和随机控制系统
图形化表示:用比较直观的结构图(方块图)和信号流图进行描述。
同一系统的数学模型可以表示为不同的形式,需要根据不同的情况对这些模型进行取舍。机理分析法:
依据系统及元件各变量之间所遵循的物理或化学
规律列写出相应的数学关系式,建立模型。
适用于比较简单的系统
实验辨识法:
人为地对系统施加某种测试信号,记录其输出响应,并用适当的数学模型进行逼近。这种方法也称为系统辨识。
适用于复杂系统
免责声明:本网站所刊载信息,不代表本站观点。所转载内容之原创性、真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考并自行核实。