1 引言随着高速铁路和城市轨道交通的迅猛发展, 列车运行引起的环境振动问题日益突出. 列车运行产生的微振动一般不会直接造成建筑物的坍塌和破坏, 但可能对建筑物内仪器设备的精度以及居民的日常生活产生很大影响. 因此, 在发展轨道交通的同时, 也急需把环境振动问题列为必须解决的关键问题之一. 许多研究表明, 列车运行时存在某一临界车速, 在该速度下地面振动响应会急剧增加. 1995 年, Krylov[1]通过理论计算发现, 当列车速度达到土体表面的Rayleigh波波速时, 地面振动响应就会发生突增. 1997 年, 瑞典国家铁路局在 Ledsgård 西海岸开展了软土振动试验, 结果表明列车运营速度达 200 km/h时十分接近该场地列车运行的临界速度[2]. 目前, 高速铁路的运营速度通常在 200~350 km/h, 法国的TGV 更是在 2007 年创下了有轨列车最高试验速度574.8 km/h 的世界记录, 列车速度超过临界速度的情况很有可能发生. 特别是, 我国很多地区的土体很软(如上海、杭州、广州、天津等), 该临界状态就更容易达到. 因此, 针对软土地基线路, 开展高速列车引起的地面振动研究具有非常重要的理论和现实意义.
2 列车运行引起地面振动的分析方法列车运行引起的地面振动问题涉及因素众多, 包括车辆、轨道结构及周围土体等. 为综合考虑各项因素的影响, 一些学者建立了整体系统模型研究列车引起的地面振动问题. 例如, 和振兴与翟婉明等人[3, 4]建立了列车-轨道-地基耦合模型, 分析高速铁路板式无砟轨道线路引起的地面振动; Xia 等人[5]建立了列车-轨道-地基动态相互作用模型, 分析移动列车中国科学: 技术科学 2012 年 第 42 卷 第 10 期1149 作用下的地面振动响应. 本文在充分考虑了各子系统之间的关联性以及数值计算的高效性前提下, 将列车引起的地面振动问题拆分成了两个子问题进行研究: 首先, 基于车辆-轨道耦合动力学理论[6], 建立列车-轨道垂向耦合模型, 分析车辆与轨道之间的动态相互作用, 获得作用于轨道结构上的激振力; 然后, 借助于 ANSYS 有限元软件建立轨道-土体有限元模型, 分析列车动荷载作用下土体的振动特性.
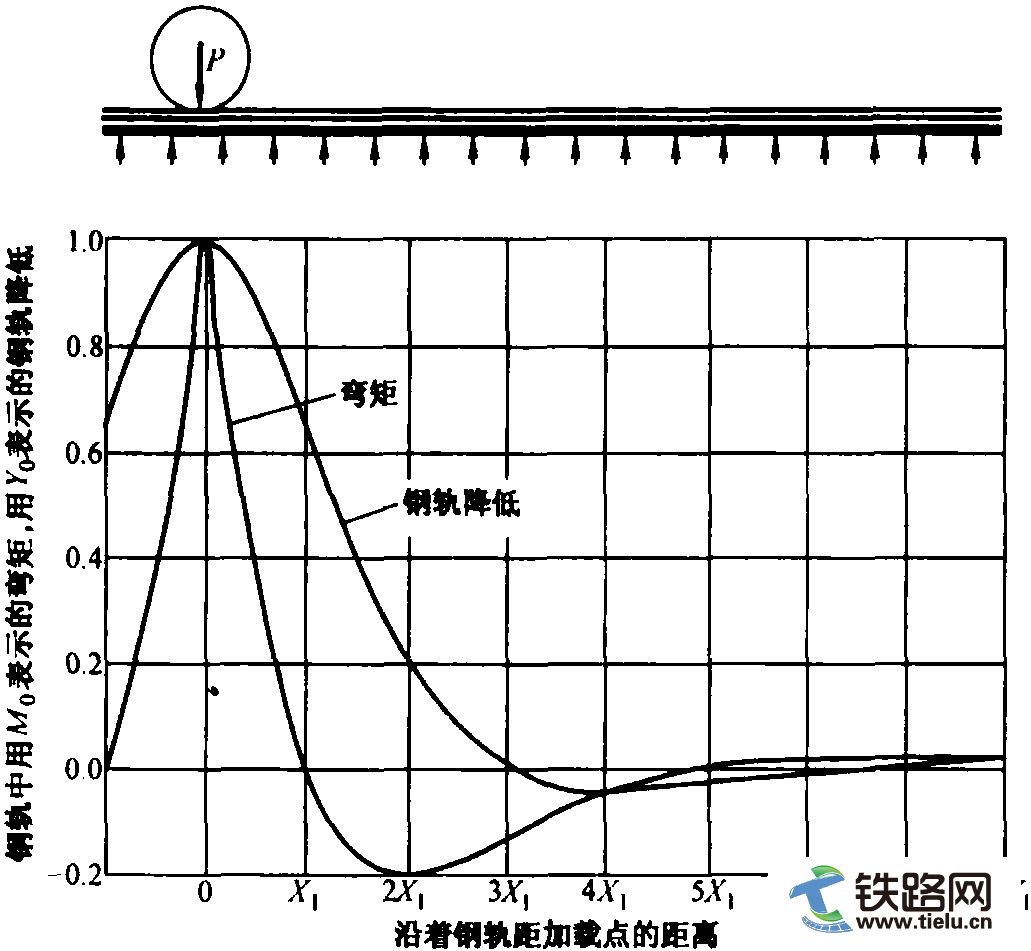
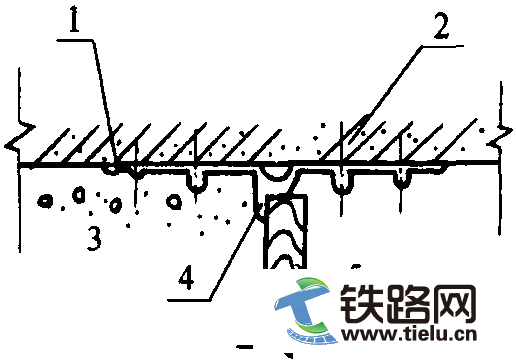
2.1 列车-轨道垂向耦合模型车辆-轨道垂向耦合动力学理论[6]是研究车辆与轨道动态相互作用, 特别是研究列车对线路动力作用的有效方法, 它能够方便地模拟各种形式的轮轨几何缺陷以及轨道随机不平顺所导致的列车对线路的动态作用力, 即线路激振源. 本文基于该理论建立了高速列车-轨道垂向耦合模型, 如图 1 所示. 其中, 各节车辆被模拟成以速度 v 运行于轨道结构上的多刚体系统, 考虑车体的沉浮与点头运动, 转向架的沉浮与点头运动, 轮对的沉浮运动, 共10个自由度. 钢轨采用连续离散点支承的 Euler 梁模拟, 轨下基础的建模因轨道结构形式的不同而有所区别. 下面重点介绍高速铁路常用的板式无砟轨道的建模. 通常在建立板式轨道振动分析模型时, CA 砂浆层以下的基础结构不再考虑, 而是直接进行固支. 由于本文所研究的地基土很软, 土体弹性可能会对轨道结构的振动产生较大影响, 因此为更真实地模拟软土线路上的行车条件, 轨道建模时考虑了底座参振及软土弹性的影响. 其中, 轨道板被简化成弹性-阻尼基础上的两端自由梁, 其振动微分方程的具体形式参见文献[6]. 底座的建模与轨道板类似, 它被简化为弹性-阻尼地基上的两端自由梁, 其垂向振动微分方程为
免责声明:本网站所刊载信息,不代表本站观点。所转载内容之原创性、真实性、完整性、及时性本站不作任何保证或承诺,请读者仅作参考并自行核实。